? Roter-Faden-Check und Korrektur der Methodik
Mehr erfahrenMethodik
Weitere Themen
- Anleitungen + Beispiele
- Bachelorarbeit
- Masterarbeit
- Dissertation
- Hausarbeit
- Seminararbeit
- Studienarbeit
- Praktikumsbericht
- Facharbeit
- Essay
- Report (Bericht)
- Kommentar
- Gutachten
- Hilfe für Akademiker
- Schneller Lernen
- Studium Klausuren
- Wissenschaftliches Schreiben
- Wissenschaftliches Poster
- Abbildungen & Tabellen
- Methodik
- Richtig Zitieren
- Plagiate vermeiden
- Richtig Zitieren
- APA 6 und 7
- Harvard zitieren
- IEEE zitieren
- Lexikon
- Experten-Ratgeber (Gratis E-Books)
- Begriffe Studium A – Z
- Geschäftsunterlagen nach DIN
- Groß- und Kleinschreibung
- Experten helfen dir 🎓
- Bücher + Kurse
- Thesis-Start-Coaching
Regressionsanalyse – Lineare, multiple lineare, logistische, multinominalie
Die Regressionsanalyse ist ein statistisches Analyseverfahren zur Untersuchung von Zusammenhängen zwischen mehreren Variablen. Es kann festgestellt werden, ob und in welchem Ausmaß eine unabhängige Variable eine abhängige Variable beeinflusst.
Auf diese Weise unterstützt die Regressionsanalyse die Entscheidungsfindung und ermöglicht es dir als Forscher, präzise Vorhersagen zu treffen, die einen tieferen Einblick in die Realität bieten.
In diesem 1a-Studi Artikel lernst du die verschiedenen Arten einer Regression sowie deren Anwendung am Regressionsmodell kennen.
Inhaltsverzeichnis
Was ist eine Regression?
Der Kern der wissenschaftlichen Arbeit zur Regressionsanalyse ist die Berechnung der Regression mittels einer Regressionsgeraden bzw. -funktion. Die Regressionsanalyse zeigt den gerichteten linearen Zusammenhang zwischen den untersuchten Variablen auf.
Hierzu wird der Wert der unabhängigen Variable verändert, und die Folgen für die abhängige Variable werden gemessen.
Je nach Art der wissenschaftlichen Arbeit zur Regressionsanalyse kann eine festgelegte Anzahl von möglichen Merkmalsausprägungen der unabhängigen Variable untersucht werden. Die Merkmalsausprägungen beschreiben den bestimmten Wert oder Zustand, den die unabhängige Variable annehmen kann.
Wird z. B. der Einfluss von Alter, Bildung und Beruf auf das Einkommen untersucht, so sind die Merkmalsausprägungen jedes Probanden das konkrete Alter, die Bildung und der Beruf.
Ziele der Regressionsanalyse
1. Herstellung von kausalen Zusammenhängen
Untersuchen, ob und in welchem Ausmaß ein Zusammenhang zwischen zwei oder mehr Variablen besteht.
2. Vorhersage von Veränderungen
Ermitteln, wie sich die abhängige Variable verändert, wenn eine der unabhängigen Variablen angepasst wird.
3. Bestimmung von Werten zu einem bestimmten Zeitpunkt
Feststellen, welchen Wert die abhängige Variable annimmt, nachdem die unabhängige Variable zu einem bestimmten Zeitpunkt neu festgelegt wurde.
Voraussetzung für die lineare Regressionsanalyse
1. Linearer Zusammenhang zwischen den Variablen
Um bei einer wissenschaftlichen Arbeit zur linearen Regressionsanalyse belastbare Ergebnisse zu erhalten, müssen die folgenden Modellannahmen erfüllt sein:
2. Metrisches Skalenniveau
Sowohl die abhängige Variable (AV) als auch die unabhängige Variable (UV) sollten auf metrischem Skalenniveau vorliegen, d. h. konkrete Zahlenwerte besitzen.
3. Abweichungen (Residuen)
Es sollten keine untereinander korrelierten Muster aufweisen und gleichmäßig über den gesamten Wertebereich der abhängigen Variable streuen.
16 professionelle Korrekturdienste 🎓
Garantiert Studium mit sehr guter Note bestehen! Lass dir jetzt vom Testsieger für wissenschaftliche Lektorate bei deinem Bachelor und Master helfen.
- 3 Textkorrekturstufen
- Zitation & Literaturverzeichnis
- Formatierung nach Richtlinien
- Präsentation (Kolloquium)
- 7 Tage bis 12 h Express

Durchführung der Regressionsanalyse:
1. Datenaufbereitung:
Im ersten Schritt überprüfst du deinen Datensatz, bevor du mit der Regressionsanalyse beginnst. Vollständige und genaue Datensätze sind entscheidend, um gültige Ergebnisse zu erhalten, die die Entwicklungen und Trends der Variablen genau beschreiben.
Dies kann erreicht werden durch:
- Überschlagsrechnungen und Plausibilitätsprüfungen.
- Ergänzung von fehlenden Daten mit Missing-Date-Techniken
- Grafische Darstellung der Daten bei Bedarf
- Übertragung der Daten in das für das Regressionsmodell erforderliche Format
2. Modellanpassung
Im nächsten Schritt wählst du das zu schätzende Modell aus und wendest die Schätzmethode an, um die Parameter zu bestimmen. Achte darauf, dass du genügend Datenpunkte zur Verfügung hast, um genaue Ergebnisse zu bekommen.
Um Abweichungen, die die Ergebnisse verzerren, zu minimieren, werden in der Regressionsanalyse Fehlerkorrekturen verwendet. Diese können durch das verwendete Modell vorgegeben werden.
Beispielsweise wird bei der linearen Regression eine lineare Funktion verwendet, um Fehlerwerte zu berechnen, die bereits im Modell berücksichtigt sind.
3. Validierung des Modells
Im dritten Schritt erfolgt die Validierung deines Regressionsmodells. Diese stellt sicher, dass dein Modell den untersuchten Zusammenhang gut erfasst.
Diese erfolgt, indem überprüft wird:
- ob das Modell die Beziehung zwischen unabhängiger und abhängiger Variable angemessen erfasst und
- wie präzise diese Erfassung ist
Zu diesem Zweck kann eine Residuenanalyse durchgeführt werden, um sicherzustellen, dass es keine systematischen Muster im Datensatz gibt, die auf nicht berücksichtigte Variablen hindeuten. Darüber hinaus kann der Datensatz in diesem Schritt u. a. auf Überanpassung oder auf Ausreißer und einflussreiche Datenpunkte untersucht werden.
4. Vorhersage von Werten
Erfüllt das Modell alle Anforderungen, kann es im nächsten und letzten Schritte für die Vorhersage von Werten genutzt werden.
Es wird zwischen zwei Prognosearten unterschieden:
- Interpolation: Vorhersagen innerhalb der Datensätze
- Extrapolation: Das Treffen von Aussagen, die über die vorhandenen Datensätze hinausgehen. Sie erfordert eine genaue Überprüfung der prognostizierten Daten
Regressionsmodell
Die Auswahl der passenden Form der Regressionsanalyse beeinflusst die Qualität deiner Ergebnisse maßgeblich und hängt stark von deiner Datenart und Forschungsfrage ab.
Im Folgenden findest du eine Zusammenstellung unterschiedlicher Modelle:
1. Einfache lineare Regression
Die einfache lineare Regression untersucht die Beziehung zwischen einer unabhängigen Variablen und einer abhängigen Variablen. Diese Beziehung ist linear, d. h. die abhängige Variable ändert sich proportional zur unabhängigen Variablen.
Diese wird verwendet, um den Zusammenhang zwischen zwei Variablen zu quantifizieren und zu interpretieren, wie beispielsweise die Untersuchung des linearen Zusammenhangs zwischen der Anzahl der Arbeitsstunden und dem erzielten Einkommen.
2. Multiple lineare Regression
Bei der multiplen linearen Regressionsanalyse werden mehrere unabhängige Variablen verwendet, um den Zusammenhang mit der abhängigen Variablen zu erklären.
Diese wird verwendet, wenn …
- der Zusammenhang zwischen der abhängigen Variable und den unabhängigen Variablen nicht linear, sondern komplexer ist.
- der Einfluss von mehrerer potenzieller Einflussfaktoren gewichtet werden soll.
Beispiel:
Analyse des Einflusses von Werbeausgaben, Preis und Markenimage auf den Produktabsatz
Plagiatsprüfung + Entfernung
Besser als deine Hochschule. Finde Plagiate, bevor es deine Hochschule macht.
- 250+ Mrd. Quellen
- Datenschutz
- Korrektur von Plagiaten 🛡️

3. Logistische Regression
Die logistische Regression ermöglicht die Modellierung der Wahrscheinlichkeit, mit der ein bestimmtes Ereignis eintritt, insbesondere dann, wenn die Voraussetzungen für die klassische lineare Regression nicht erfüllt sind.
Die logistische Regression wird verwendet, wenn die abhängige Variable kategorial ist und nur zwei oder endlich viele Werte annehmen kann. Dies ist besonders relevant, wenn das Interesse darin besteht, die Wahrscheinlichkeit des Eintretens eines bestimmten Ereignisses zu modellieren.
Beispiel:
Prognose der Wahrscheinlichkeit einer Krankheit aufgrund von diagnostischen Tests
4. Multinominale logistische Regression
Die multinominale logistische Regression ist eine statistische Methode, die verwendet wird, wenn die abhängige Variable kategorial ist und mehr als zwei mögliche Kategorien hat.
Im Gegensatz zur binären logistischen Regression, die für zwei Kategorien geeignet ist, ermöglicht die multinominale logistische Regression die Modellierung und Vorhersage von Wahrscheinlichkeiten für mehrere Kategorien.
Dieses Modell ist gut geeignet, wenn die abhängige Variable nicht binär, sondern in mehrere Kategorien unterteilt ist, wie beispielsweise bei der Einteilung von Personen in verschiedene Einkommensgruppen auf der Grundlage mehrerer Faktoren.
Vergleich der Regressionsarten
| Eigenschaft | Einfache lineare Regression | Multiple lineare Regression | Logistische Regression | Multinominale logistische Regression |
|---|---|---|---|---|
| Anzahl der AV | 1 | 1 | Mindestens 2 | Mindestens 3 |
| Anzahl der UV | 1 | Mindestens 2 | Mindestens 2 | Mindestens 2 |
| Art der AV | - | metrisch | - | dichotom intervallskaliert diskret |
| Art der UV | - | metrisch | metrisch ordinal dichotom | beliebig |
| Ziel | Vorhersage der Beziehung zwischen AV und UV | Vorhersage der Beziehung zwischen mehreren UV auf eine AV | Vorhersage der Wahrscheinlichkeit für ein binäres Ereignis | Vorhersage von Zusammenhängen zwischen abhängiger und kategorialer Variable und mehreren unabhängigen Variablen |
Einfache lineare Regression
Die einfache lineare Regression wird angewandt, wenn Forscher den Einfluss einer einzelnen Variable auf eine Zielgröße verstehen möchten, ohne die Komplexität mehrerer Variablen in Betracht zu ziehen.
Diese lässt sich anhand des folgenden Modells modellieren:

- Y: abhängige Variable, die vorhergesagt werden soll
- ß₀: der y-Achsenabschnitt, der den Wert von Y angibt, wenn X = 0 ist.
- ß₁: der Regressionskoeffizient für X
- X: die unabhängige Variable
- Ei: Fehlerterm, der die Abweichungen zwischen den gemessenen Werten von Y und den prognostizierten Werten angibt.
Die einfache lineare Regression versucht die treffendste Schätzung von ß₀ und ß₁ zu ermitteln, um die Beziehung zwischen den Variablen zu bestimmen.
Formatierung nach Richtlinien
Deine Bachelorarbeit, Hausarbeit, Masterarbeit 100 % nach den Richtlinien formatiert.
- Von Deckblatt bis Anhang
- Seitenzahlen (römisch/arabisch)
- Kopf- & Fußbereich u.v.m.
- druck- und abgabefertig

Regressionsanalyse Beispiel
In deiner Hausarbeit möchtest du verstehen, wie sich die Anzahl der Stunden, die jemand für das Studium aufwendet (unabhängige Variable), auf die Note in einem Kurs (abhängige Variable) auswirkt. Dafür sammelst du Daten von verschiedenen Studenten und analysierst diese mit einer einfachen linearen Regressionsgleichung:

Dabei sind;
- Y die Kursnote
- X Anzahl der Stunden, die zum Studieren verwendet wurden
- ß₀ der durchschnittliche Notenwert, der ohne Studium erreicht wurde
- ß₁ gibt an, wie sich die Note ändert, wenn die Anzahl der Studienstunden um eine erhöht wird
- u repräsentiert den Einfluss, der durch andere Variablen besteht, die die Note beeinflussen können (z. B. Ablenkung). In unserer Untersuchung werden diese nicht beachtet.
Die Regressionsgleichung könnte so aussehen:

Die Interpretation der Ergebnisse zeigt, dass der durchschnittliche Notenwert ohne Studienzeit 75 beträgt. Der Koeffizient ß₁ von 2 bedeutet, dass der Notenwert mit jeder zusätzlichen Studienstunde die Note um 2 Punkte steigt.
Quadratische RAQuadratische Regression
Bilden die erhobenen Datenpunkte keine Gerade wie bei der linearen Regression, sondern eine Parabel mit einer Symmetrieachse parallel zur y-Achse, so ist das Modell der quadratischen Regression geeignet.
Der Zusammenhang zwischen unabhängiger und abhängiger Variable ist in diesem Fall nicht linear. Eine Annäherung des Zusammenhangs ist mit quadratischen Termen wie folgt möglich:

Die Methode der quadratischen Regression wird verwendet, um die besten passenden Werte für a, ß₁ und ß₂ zu finden, die die Summe der quadrierten Abweichungen (Residuen) zwischen den beobachteten und den vorhergesagten Werten minimieren.
Dazu wird häufig die Methode der kleinsten Quadrate verwendet, bei der aus einer Datenpunktewolke eine Kurve ermittelt wird, die möglichst nahe an den vorhandenen Datenpunkten liegt.
RegressionsgleichungRegressionsgleichung
Die Regressionsgleichung für eine einfache Regression lautet:

Dabei ist Y der Wert abhängige Variable und x der Wert der unabhängige Variable.
Letztere wird durch den Regressionskoeffizienten ß bestimmt. ß drückt die Steigung der Regressionsgeraden aus. Sie gibt die Änderung der abhängigen Variablen bei Änderung der unabhängigen Variable an. Ein größerer Zahlenwert von ß bedeutet einen größeren Einfluss der unabhängigen Variablen auf die abhängige Variable.
Für die Schätzung der Regressionskoeffizienten eignet sich die Methode der kleinsten Quadrate, die Summe der quadrierten Residuen minimiert werden.
Die Regressionskonstante ß₀ stellt den Wert von AV dar, wenn UV den Wert Null hat. Diese sollte nur dann inhaltlich interpretiert werden, wenn die UV tatsächlich Null sein kann.
a definiert den Ausgangspunkt der Regressionsanalyse. u beschreibt den Fehlerwert, d. h. den Effekt, der nicht durch die UV erklärt werden kann.
Interpretation der Regressionsgeraden
Die Regressionskoeffizienten werden folgendermaßen interpretiert:
„Wenn die unabhängige Variable X um eins erhöht wird, wird eine Änderung der abhängigen Variable y um β Einheiten beobachtet, vorausgesetzt, dass alle anderen unabhängigen Variablen konstant bleiben.“
Regressionsgeraden einer multiplen Regressionsanalyse:
Bei einer multiplen Regressionsgleichung wird für jede unabhängige Variable ein weiterer Regressionskoeffizient hinzugefügt:
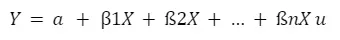
So kann der Einfluss mehrerer unabhängiger Variablen in einer linearen Funktion untersucht werden.
Häufige Fragen & AntwortenDu hast noch weitere Fragen zum Thema Methodik in wissenschaftlichen Arbeiten, die du nicht in diesem Artikel beantwortet bekommen hast? Dann recherchiere weiter in der 1a-Studi Akademie.


